
ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club
三平方の定理の解説 直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。 ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。仙台公演のるっさんのソロパートはすと9のなかで唯一オリ曲じゃなくて、ボカロカバーだったんだよね(イノコリ先生)。 ここにきてそのボカロ曲が歌われるとはこれまた鳥肌だったし凄すぎたんだわ👏
三 平方 の 定理 表
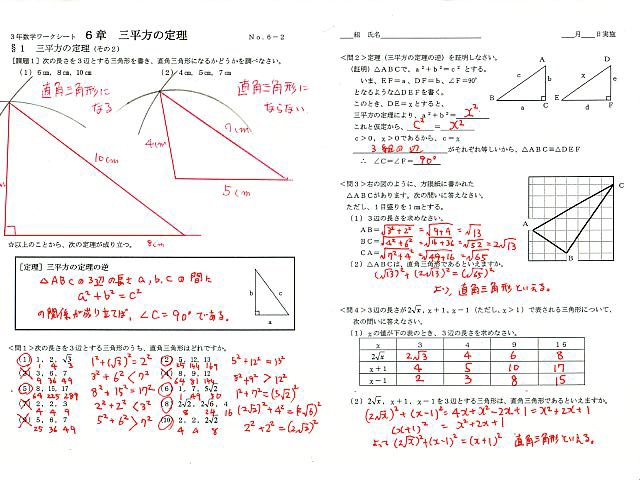
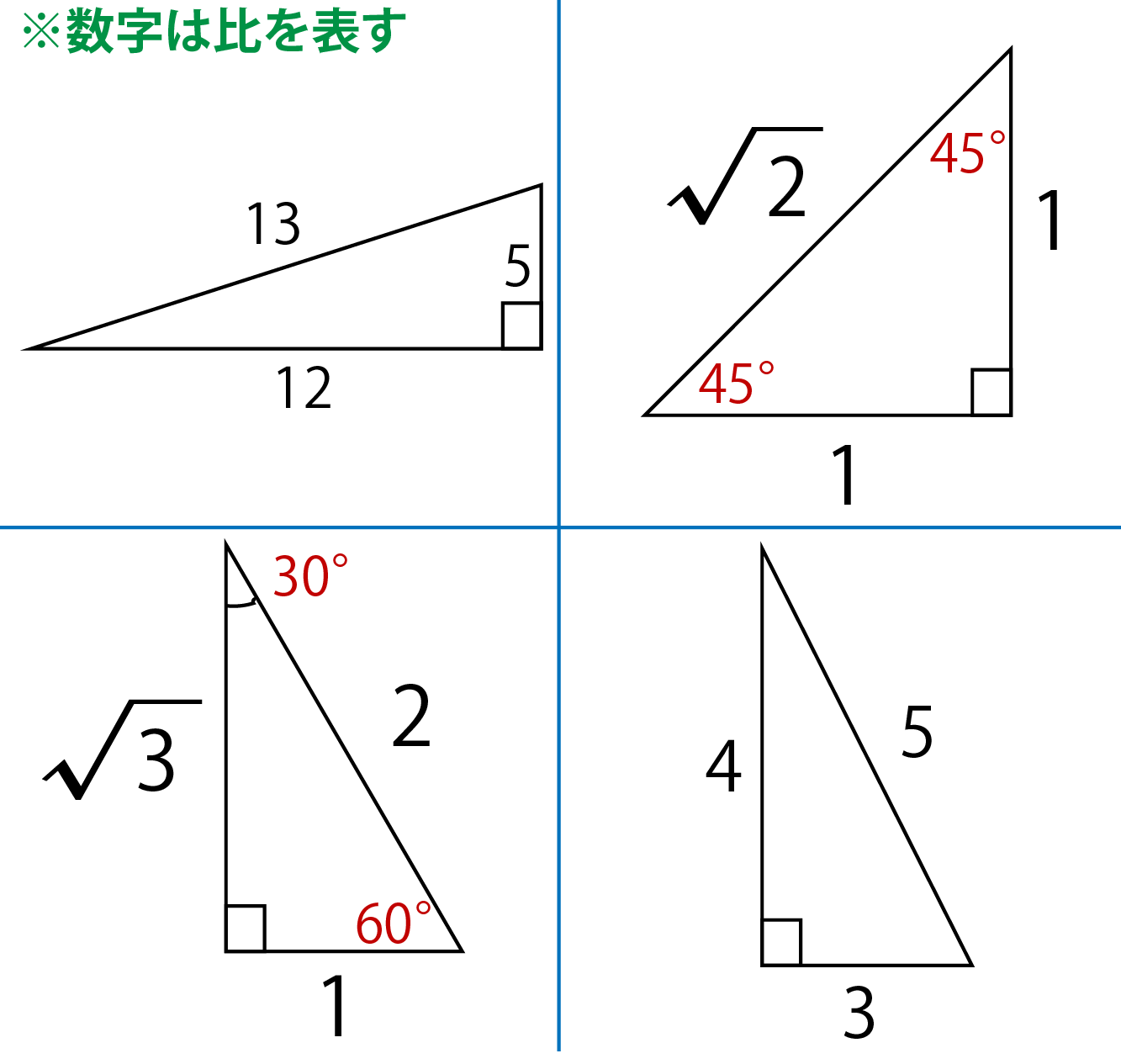
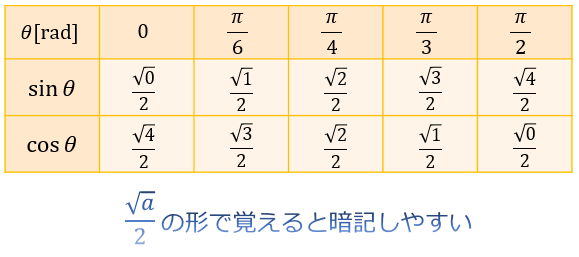
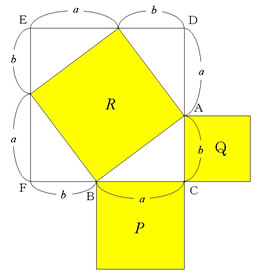
三 平方 の 定理 表-直角三角形では,2つの辺の長さがわかると,三平方の定理を使って他の1辺の長さが計算できることを覚えておきましょう。 また,三平方の定理の逆も成り立ちます。3辺の長さがa,b,cの ABCにおいて,a 2 b 2 =c 2 が成り立つならば, ABCは直角三角形である これらの形を暗記すると、よりスピーディに計算できるようになります。 もちろん、万が一それぞれの辺の比を忘れてしまっても、直角三角形の \(2\) 辺の長さがわかっていれば、もう \(1\) 辺の長さは三平方の定理で導き出せるので、あわてないでくださいね。

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。 なので、実際にこの定理で辺の長さを計算三平方の定理 (さんへいほうのていり) 直角三角形の辺に関する「 ピタゴラスの定理 」のこと 「 三個の平方数の和 」で表される数に関する定理のこと このページは 曖昧さ回避のためのページ です。 一つの語句が複数の意味・職能を有する場合の 三平方の定理(ピタゴラスの定理): \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem 105個の中で,個人的に「簡単で
今回は『三平方の定理』という単元を 基礎から解説していきます。 三平方の定理は、いつ習う? 学校によって多少の違いはありますが 大体は3年生の3学期に学習します。 中3の終盤に学習するにも関わらず 入試にはバンバンと出題されてきます。 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。
三 平方 の 定理 表のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
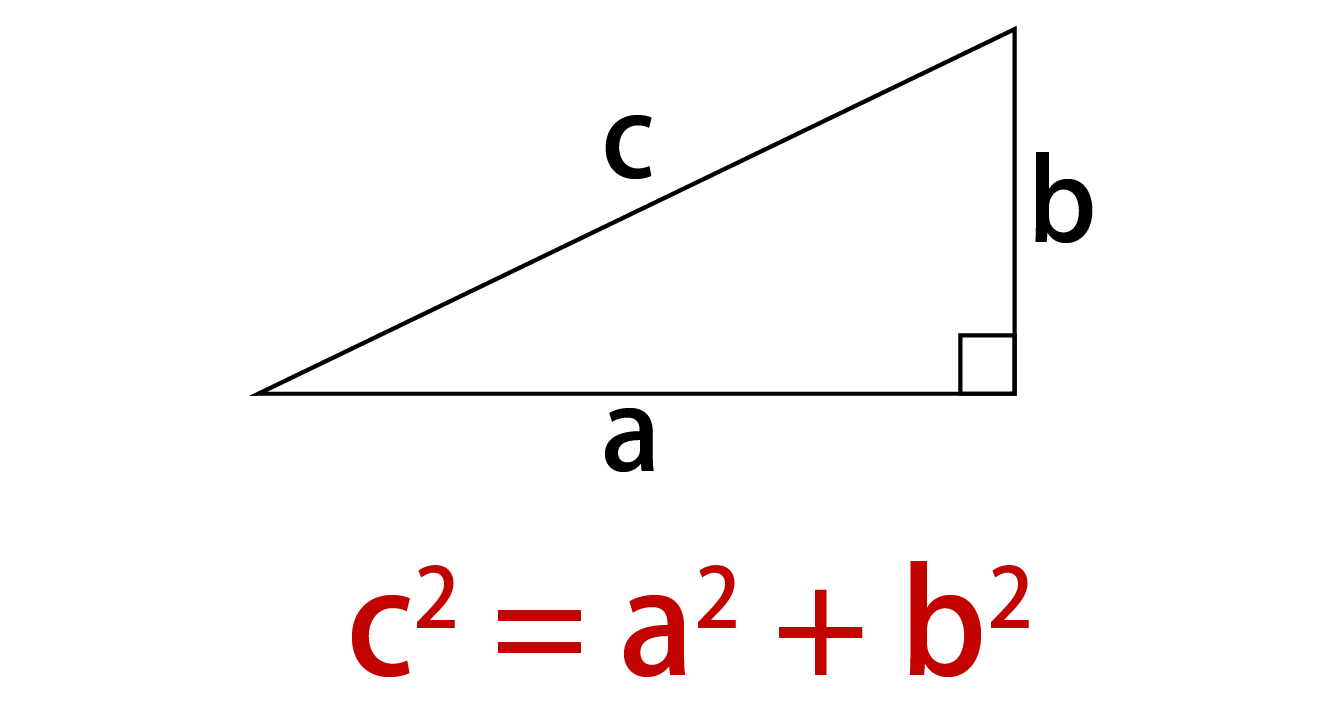 |  | |
 |  | |
 |  | |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
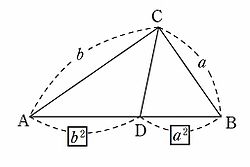 |  |
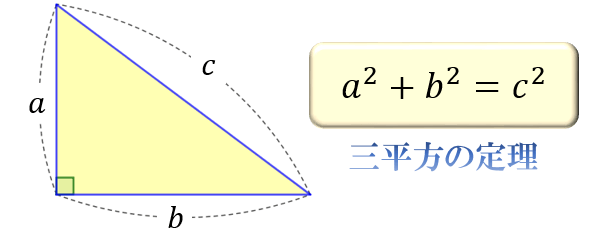
三平方の定理を使えば,直角三角形の2辺の長さが分かれば残りの1辺の長さが求められる. たとえば右図では, b , c が分かっていれば a が求められる. 多変数二次の不定方程式について (2) p 進平方数, 三平方和定理 正の整数 𝒏 が三つの平方数の和に表されるための 必要充分条件 は, 𝒏 から 4 を成るべく多く抽出して 𝒏 = 4 ᵏ ℓ と書いたときに, ℓ ≢ 7 (mod8) になることである この連続記事は以下を





0 件のコメント:
コメントを投稿