
この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 数学 教えて Goo
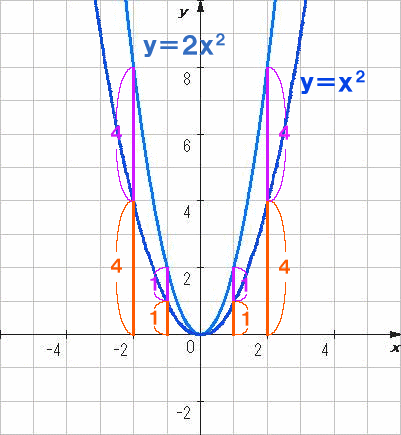
このように y =2 x ²のグラフを ヨコが-3から2の部分で切り取ります。 y の変域を求めなさい ⇒ グラフのタテの範囲はどうなる? ヨコの範囲で切り取ったグラフを見て タテの範囲がどうなっているかを見ます。 x =-3のときの座標は y =2 x ²に代入してやると求めることができますね。 y =2× (-3)²=2×9=18 それを利用してやると、縦の範囲は 0から18となっています。 よって、 y の変域 そして、すっごく安い! ! このサイト作成や塾講師としてのお仕事に役立てています。 なので、ぜひとも体験していただきたい (^^) ⇒ スタディサプリの詳細はこちら 関数y=ax2乗変化の割合と裏ワザ公式について解説! y=ax2乗の利用平均の速さ
Y=x2乗+1 グラフ
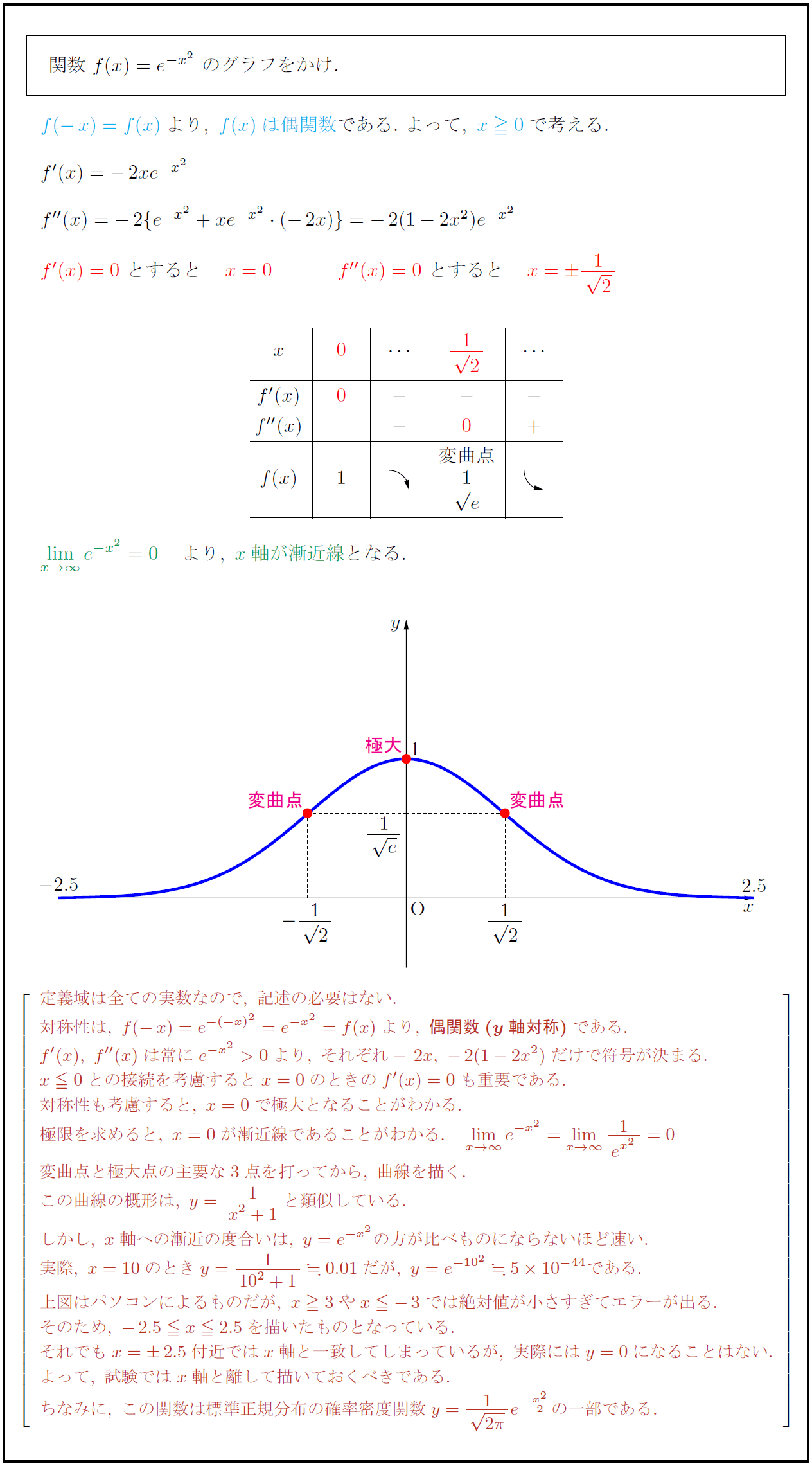
Y=x2乗+1 グラフ-※通常、 の定義域は ですから、「 のグラフを描け」という問題で上記のように負の部分を描いてしまうとおそらく減点されるか0点になりますので、ご注意下さい。 (追記) 上のグラフは、 は実数範囲、 は複素数範囲となっていて中途半端ですね。 も複素数範囲で考えると が分子が奇数でY=ax2乗のグラフ書き方 まとめ お疲れ様でした! 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ! これだけですね。 何度も練習すれば 誰にでも簡単に書けるようになります。 レッツ! 練習 (/・ω・)/

関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube
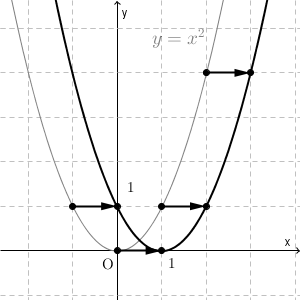
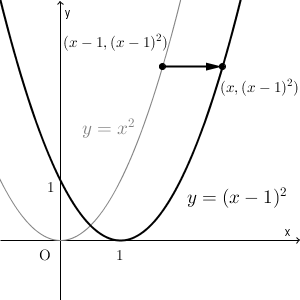
y = a x 2 q のグラフは、 y = a x 2 のグラフを y 軸方向に q だけ移動したものである 基本二次関数 y=ax^2 のグラフ では、放物線の頂点と軸の紹介をしました。 二次関数 y = a x 2 q については、上の図からもわかる通り、軸は y 軸、頂点の座標は ( 0, q無理関数とそのグラフの書き方 レベル ★ 基礎 いろんな関数 更新日時 無理関数 の意味と,グラフをすばやく描く方法を紹介します。 慣れれば y=\sqrt {2x4}1 y = −2x 4 1 のような無理関数のグラフを10秒で描けます。 目次 無理関数とは 無理 二次関数y=ax2のグラフの書き方がわからない! みんな、元気にしてる?そらだよ☆彡 今日は二次関数y = ax2 のグラフをかくんだ! どちらかというと、今日は「絵を描く」感覚(^_)☆ え?絵を描くの苦手? 大丈夫だよ、グラフは絵とはべつものだし!
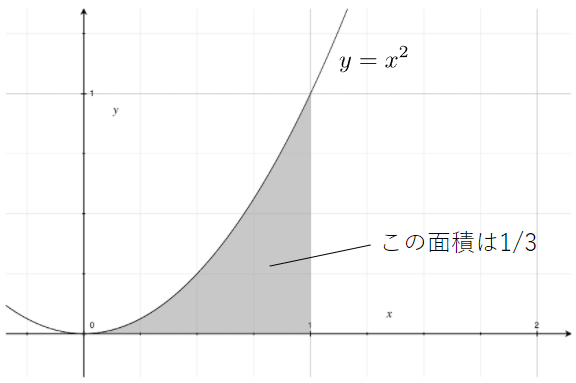
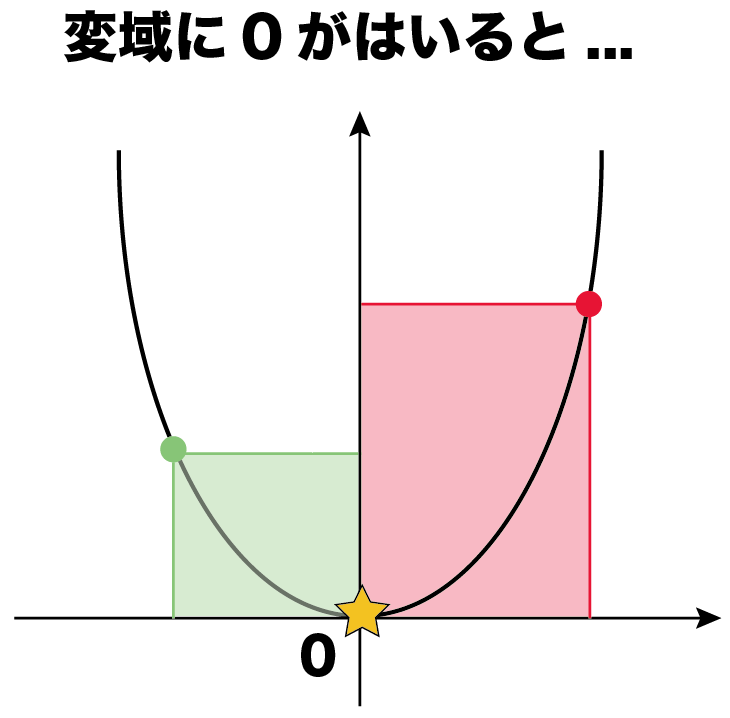
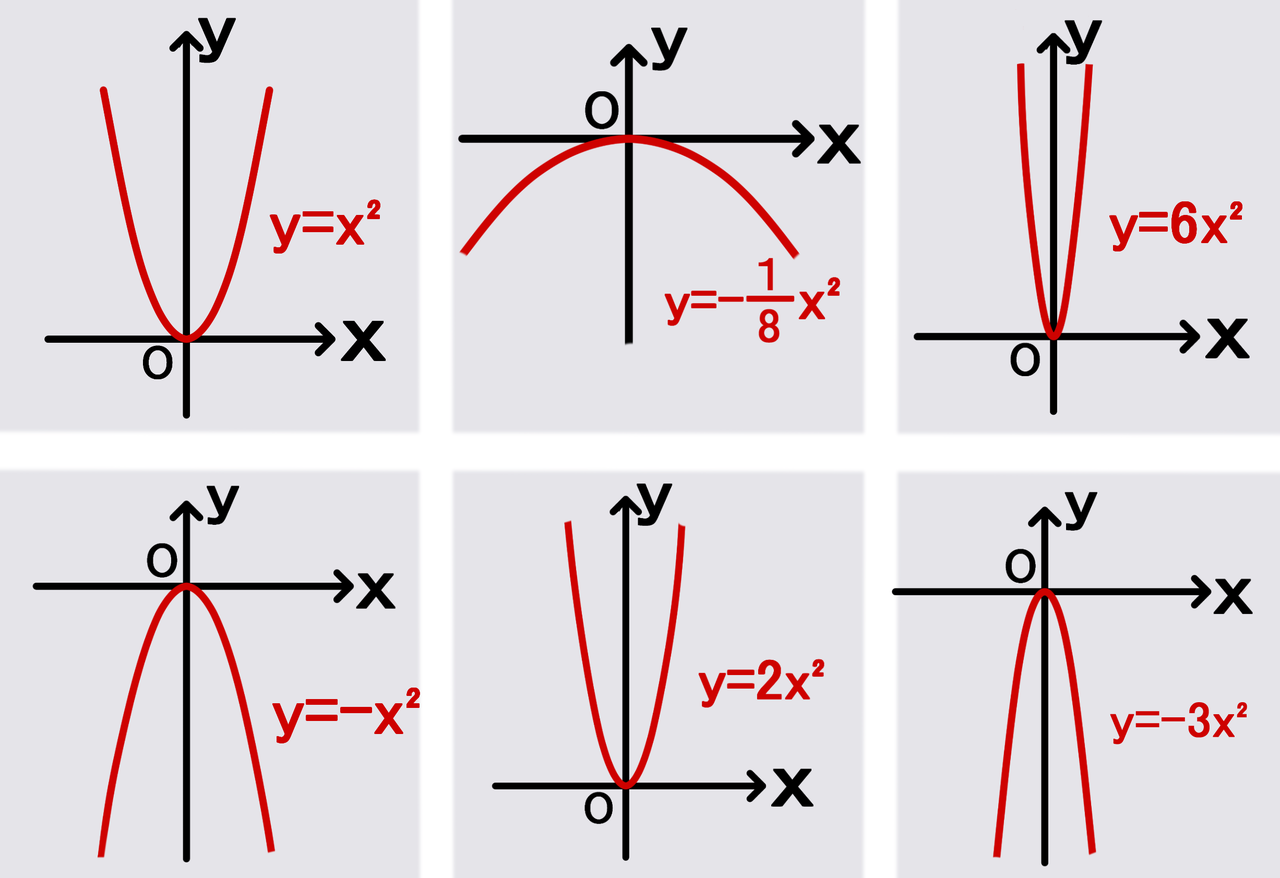
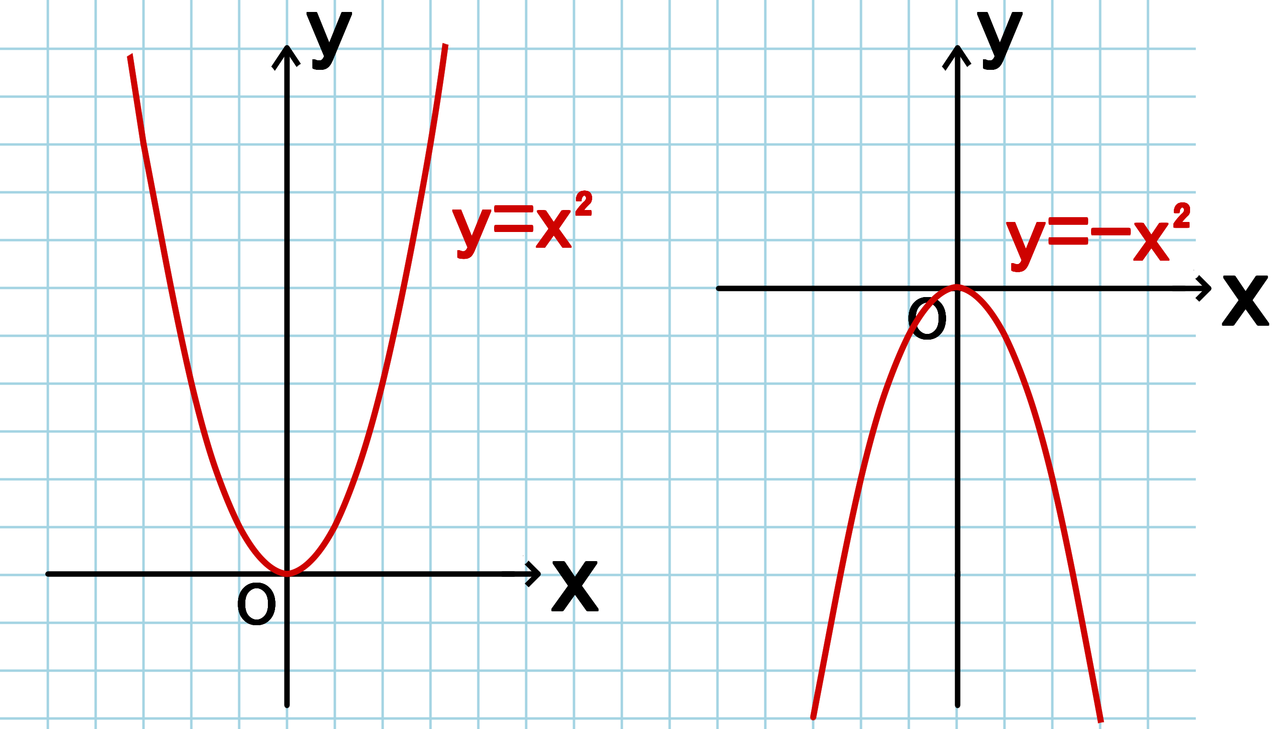
面積 解説 (ア) y=f(x)のグラフがx軸よりも上にあるとき (f(x)≧0のとき)定積分は面積を表わします。 (イ) y=f(x)のグラフがx軸よりも下にあるとき (切り紙のイメージで考えます。) (エ)2曲線の間にある図形の面積になります2乗に比例する関数は、 放物線 (ほうぶつせん)と呼ばれる線を描きます。 なぜなら、aY = f (x) y = f ( x) のグラフを、 x x 軸方向に p p y y 軸方向に q q 平行移動すると、 y− q = f (x− p) y − q = f ( x − p) になる。 これは、 2 2 次関数以外のあらゆる関数に成り立つことです。 今後も様々なところで出会うことになるでしょう。 なぜこれが
Y=x2乗+1 グラフのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | 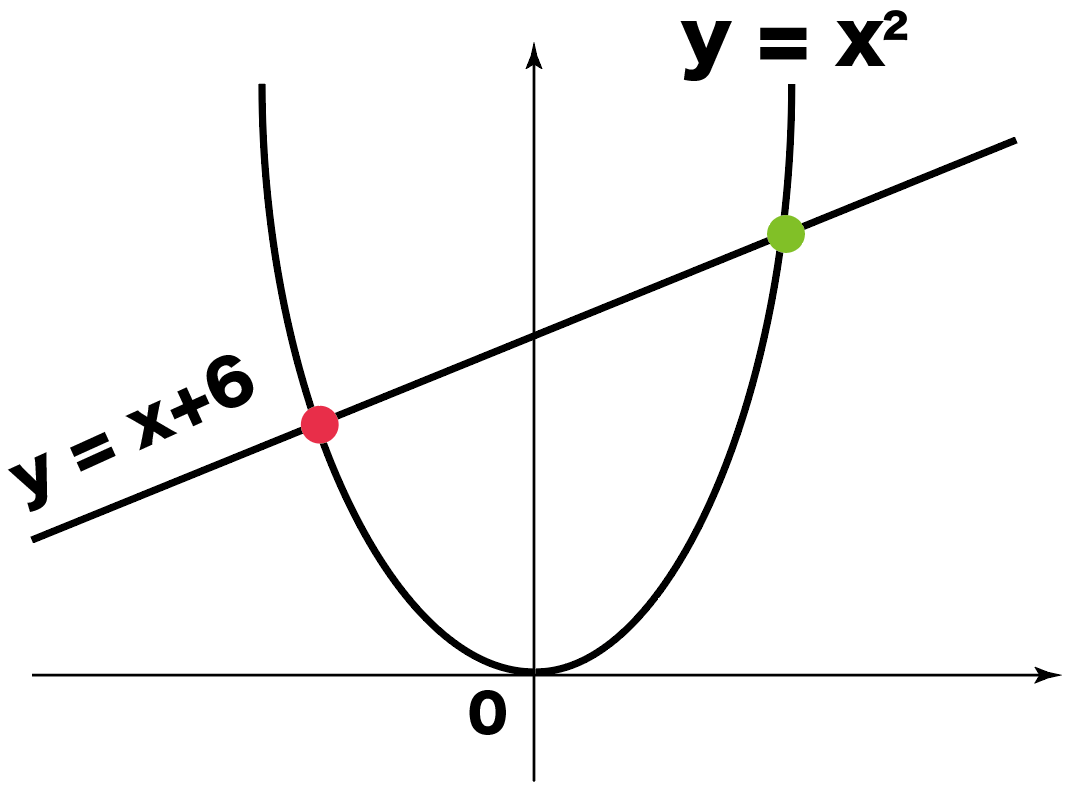 |  |
 |  | |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
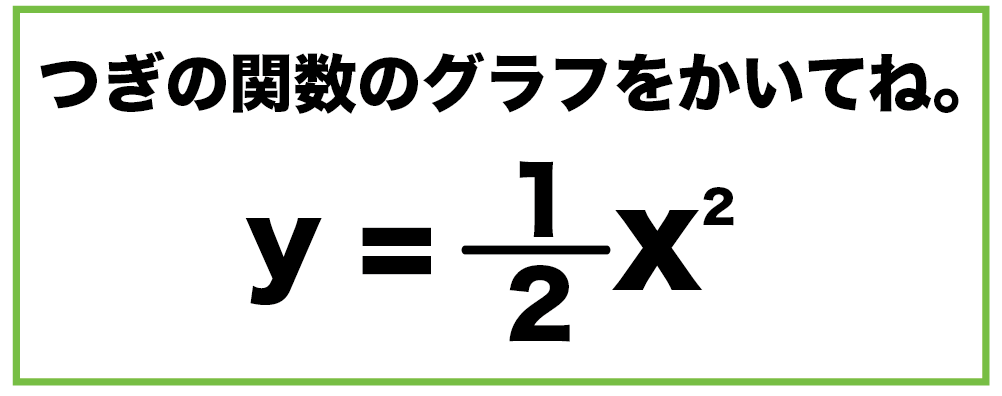 | ||
 |  |  |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「Y=x2乗+1 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
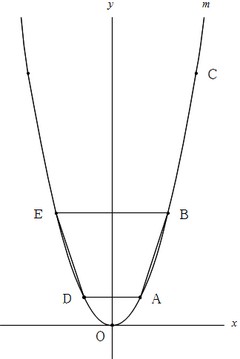
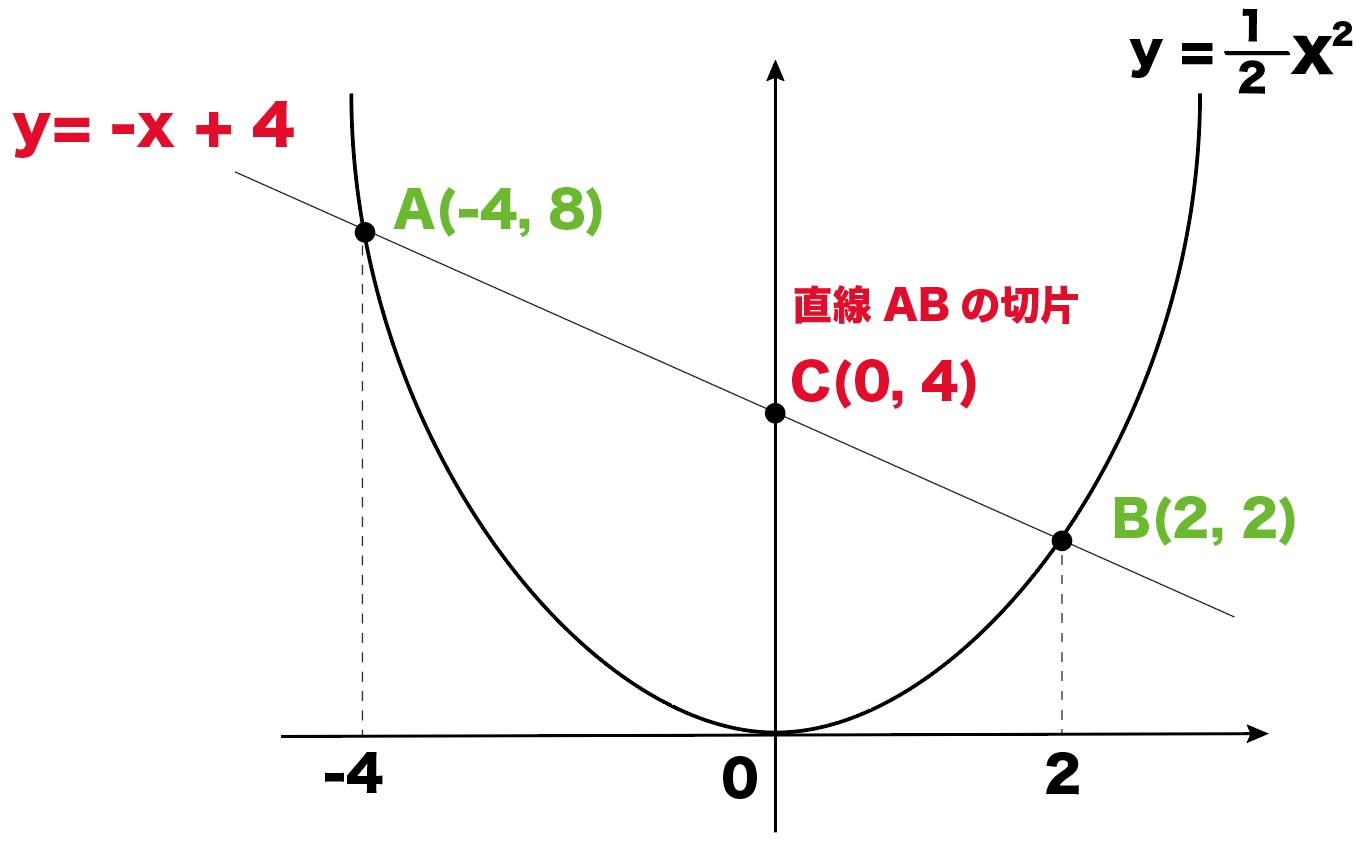
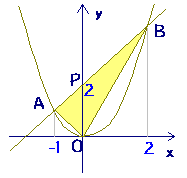
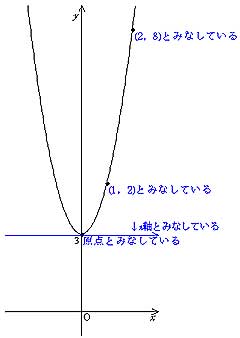
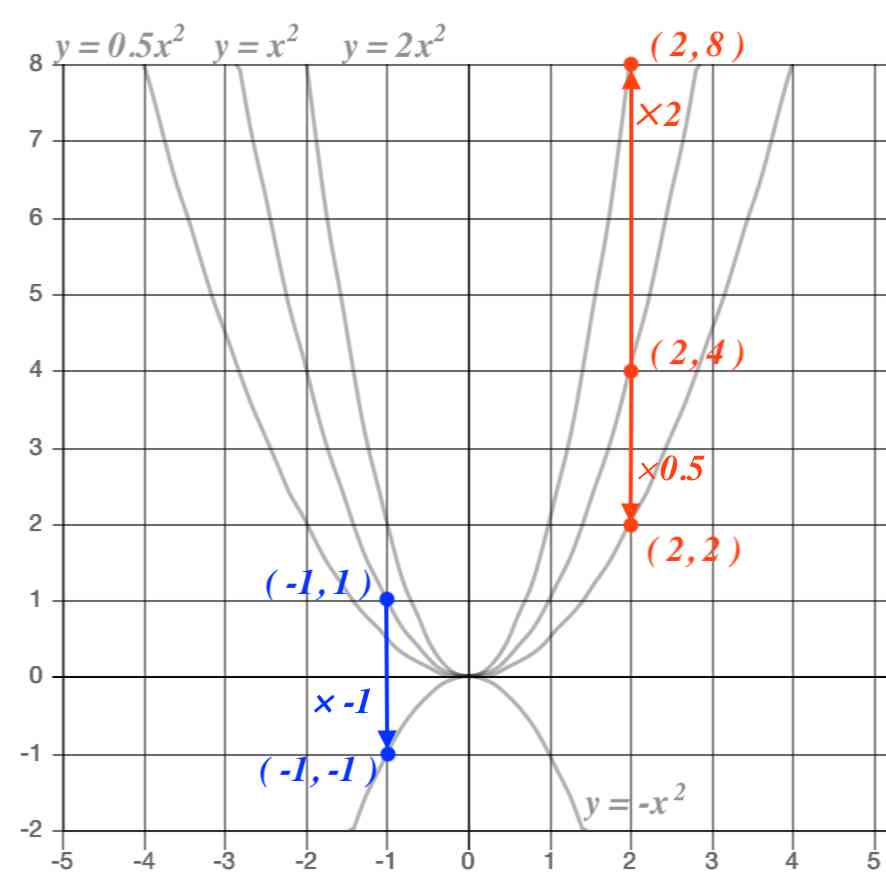
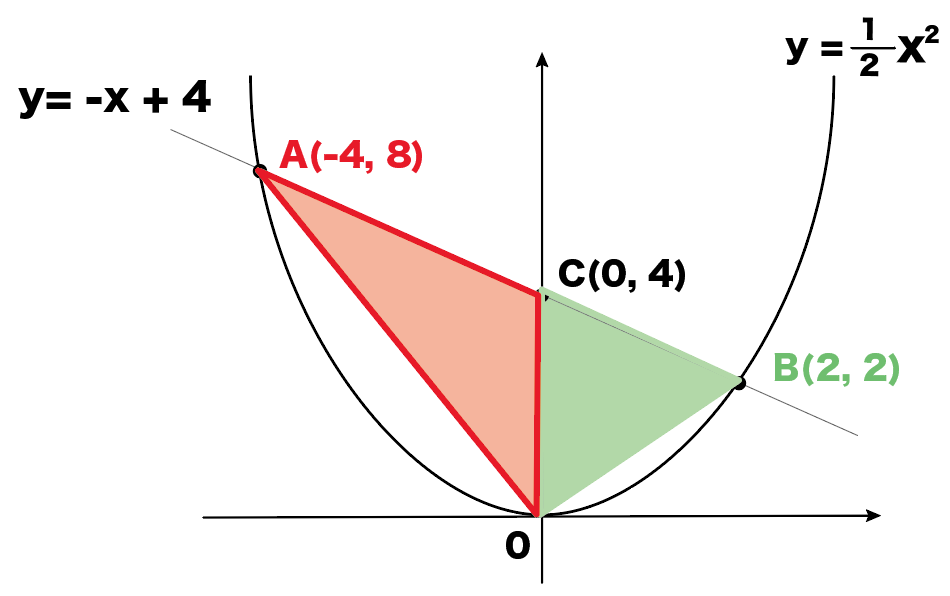
Y=ax 2 のグラフ1 A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB (両端を含む)と交わるようなaの値の範囲を求めよ。 A (2,1), B (2,8) A (4, 4), B (4, 8) A (3, 1), B (3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が4, Bのx座標が2のとき、aの値を求めよ。 A B l m n x y O 2文献 ・『岩波数学入門辞典』平方根(p543) ・吉田栗田戸田『高等学校数学I』(p53) 上記2文献では、「R=(-∞,∞) で定義された1変数関数 y=f (x)= x 2 」による実数yの逆像を平方根と呼び、 実数y>0のとき、二つある平方根のうち、正のほうを√yで表すとしている。
Incoming Term: y=x2乗 グラフ, y=x2乗 グラフ 特徴, y=x2乗 グラフ 書き方, y=x2乗+1 グラフ, y=x2乗+2x グラフ, y=x2乗-3 グラフ, y=x2乗-4x+3 グラフ, y=x2乗+2 グラフ, y=x2乗+4x グラフ, y=x2乗-4 グラフ,




0 件のコメント:
コメントを投稿